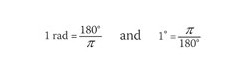我們通常測量度角，，三維化學處理時，這是約定俗成。但是，也有其他情況下，當使用不同的角度單位是更方便的。這是，這是由簡單的關系的程度有關的弧度

是熟悉的常數，對于大多數用途而言，可以被視為具有3.142的值，或22/7。 

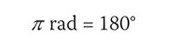
在三角學的角度和弧度使用并不是沒有問題，但對于大多數用途而言，這些可以忽略不計的定義，是令人滿意的。這直接導致進一步的關系，如：

　　片刻的思想表明弧度測量的角度度比測量值低得多。這可以第一次會面時感到迷惑。學生記住的最重要的事情是，電子計算器，可以設置在弧度（RAD）或學位（DEG）模式來操作，重要的是知道如何從一個切換到另一個模式是目前設定。

　　大多數應用涉及三角化學需要的正弦函數的使用。這被定義為直角三角形的角度 而言，由

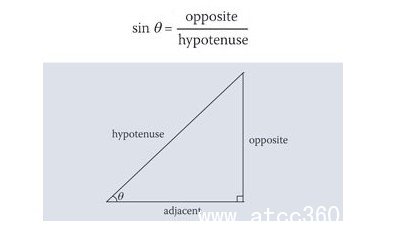雖然已被引入的功能的其他方式說明。

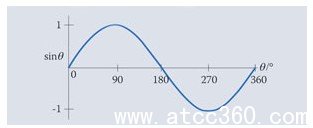
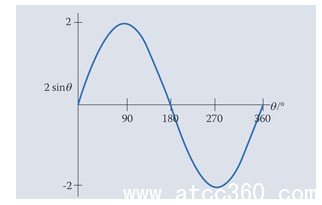
從0到360°的角度的正弦函數的曲線圖如下所示。功能并實際上重演每360°或2   弧度，并且被定義為任意角度，積極或消極的，因此，所述周期。這也是值得注意的，它有一個振幅為1，也就是說，它的范圍從-1到1。 

的功能2罪具有原函數的振幅的兩倍，也就是說，它被拉伸在垂直功能，這樣它取值范圍從-2到2。